Developers Squared : Part 1
At work, we've been discussing the best time to add developers to a team. I'm of the "later but not too late" school. It's been suggested that if I'm going to run around saying things like "later but not too late", I'm obliged to explain myself. I'm planning to write up a couple of blog entries on this topic, I'll stick to the basics in this one.
Fred Brooks in his legendary The Mythical Man-Month: Essays on Software Engineering discusses the problem of staffing and the division of work. Brooks presents his discussion as a series of graphs showing the time to complete a project versus the number of workers assigned to the project.
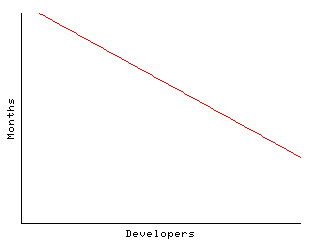
A "perfectly partionable task" is one where there is no communication between workers and no sequential constraints between subtasks. This is in all ways totally unlike a software project, and is presented for comparison only. The graph is log-log, so the 1/x relationship shows up as a straight line:
An unpartionable task (the usual example is bearing a child) takes the same amount of time (nine months) no matter how many workers are assigned. Software projects aren't generally quite this bad:

If a task is imperfectly partionable, costs associated with coordinating the subtasks have to be factored in. Communication costs vary, but Brooks models the worst case as rising with the square of the number of developers (if each worker has to spend a portion of their day talking to every other worker) Real-life software projects are generally of this variety, at least early on. Things can get ugly fast. The graph is again log-log, so it can be directly compared to the "perfectly partionable" case above:
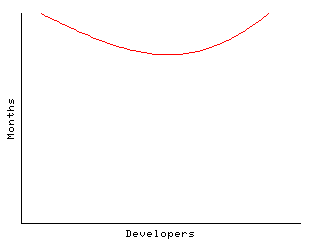
That upturn there at the end means that each additional worker actually delays the project by some amount. There is hope. The longer you wait to add people, the more mature the system framework becomes, and the more partionable the the system should be. So the "later" part in "later but not too late" has something to do with having a relatively mature system framework. I'll address the "too late" part, as well as as some other contributing factors, in upcoming postings.
tags:software,engineering,brooks,2005,july,blog,system,project
Fred Brooks in his legendary The Mythical Man-Month: Essays on Software Engineering discusses the problem of staffing and the division of work. Brooks presents his discussion as a series of graphs showing the time to complete a project versus the number of workers assigned to the project.
A "perfectly partionable task" is one where there is no communication between workers and no sequential constraints between subtasks. This is in all ways totally unlike a software project, and is presented for comparison only. The graph is log-log, so the 1/x relationship shows up as a straight line:

An unpartionable task (the usual example is bearing a child) takes the same amount of time (nine months) no matter how many workers are assigned. Software projects aren't generally quite this bad:

If a task is imperfectly partionable, costs associated with coordinating the subtasks have to be factored in. Communication costs vary, but Brooks models the worst case as rising with the square of the number of developers (if each worker has to spend a portion of their day talking to every other worker) Real-life software projects are generally of this variety, at least early on. Things can get ugly fast. The graph is again log-log, so it can be directly compared to the "perfectly partionable" case above:

That upturn there at the end means that each additional worker actually delays the project by some amount. There is hope. The longer you wait to add people, the more mature the system framework becomes, and the more partionable the the system should be. So the "later" part in "later but not too late" has something to do with having a relatively mature system framework. I'll address the "too late" part, as well as as some other contributing factors, in upcoming postings.
tags:software,engineering,brooks,2005,july,blog,system,project
You should follow me on twitter here.


0 Comments:
Post a Comment
<< Home